Multi-Agent Path Finding algorithms

This is a test post.

Table of Content

Intro

Consider 2d grid path finding problem

A*

• Multi-agent A*: plan in Joint configuration space of all robots
• Advantage: optimal
• Disadvantage: high dimensionality

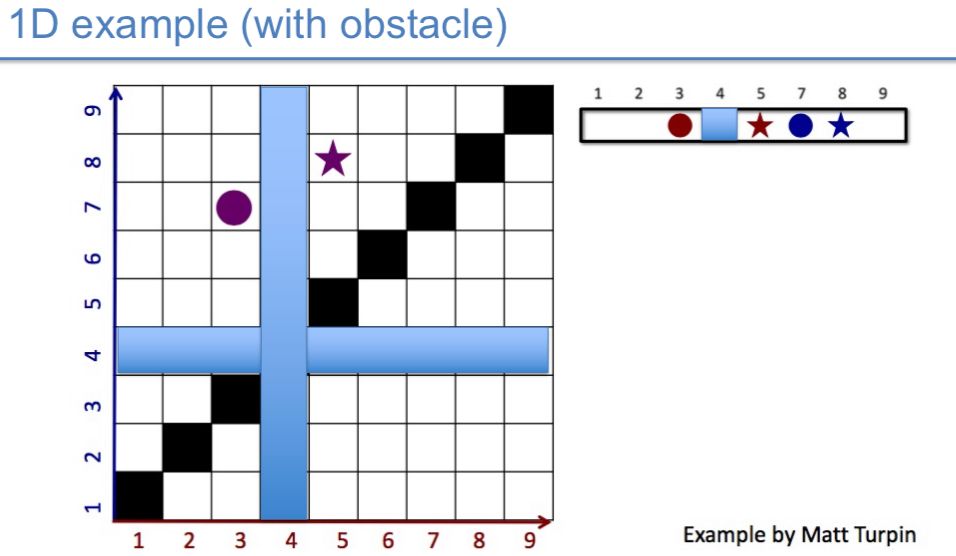
Cooperative A* (CA*)

• Each robot plans sequentially and reserves the cell it’s going to use

• Decouple cooperative path finding problem into a series of single agent searches

• Use reservation table as shared knowledge: reservation table is a sparse data structure marking off spatio-temporal regions.

• Algorithm

  1. execute A* for one agent
  2. mark off planned trajectory in reservation table (whole trajectory + duration)
  3. execute A* for other agents

• Disadvantages

  • Suboptimal
  • incomplete
  • small scale (may fail when dealing with many agents)
  • runtime slow
  • performance relies on the ordering of the robots

• Extension

  • Hierarchical CA*: use a better heuristic than Manhattan distance
  • Windowed HCA*: plan with time windows and interleave planning and execution

A* + Operator Decomposition (OD)

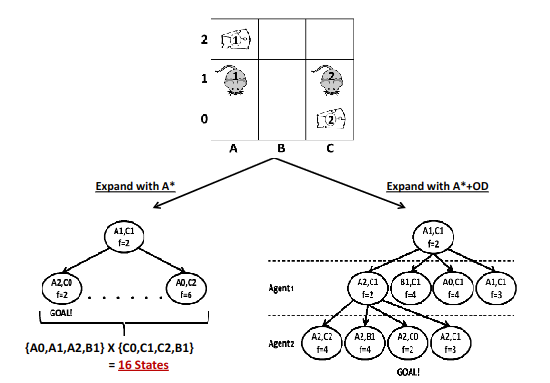
OD: reduce the search-space by allowing one agent can move at a time.

• reduce the dimensionality but increase the depth of search tree

A* + Independence Detection (ID)

A*: exponential in the number of agents, may not able to find feasible solution

ID: reduce the search-space by grouping agents together (travel groups) which do not have conflicts between each other

可以组内撞不可以组间撞，目的是将大问题分解成很多小问题。

• Single group? will be marked as
• How to plan after grouping?

ID 只管分组不管搜图

• refinement 1: illegal move table (similar to reservation table in CA*)
• refinement 2: conflict avoidance table 存储尚未分组的所有移动，以避免将来改组 (algorithm should choose path with fewest conflict avoidance table violations)

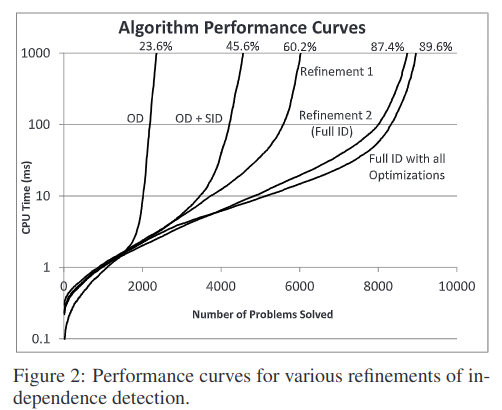
10000 problems with a random number of agents between 2 and 60.

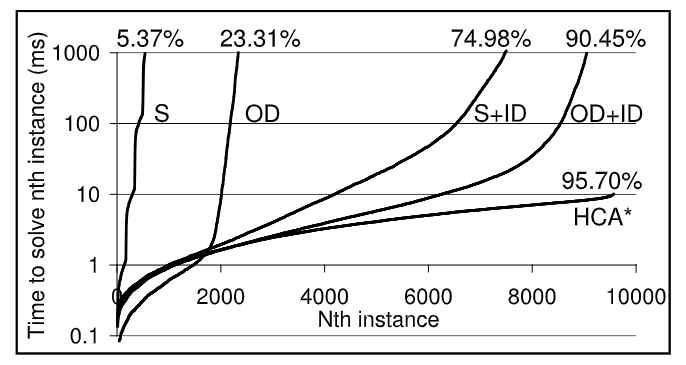
S: standard algorithm (A* baseline)

M*

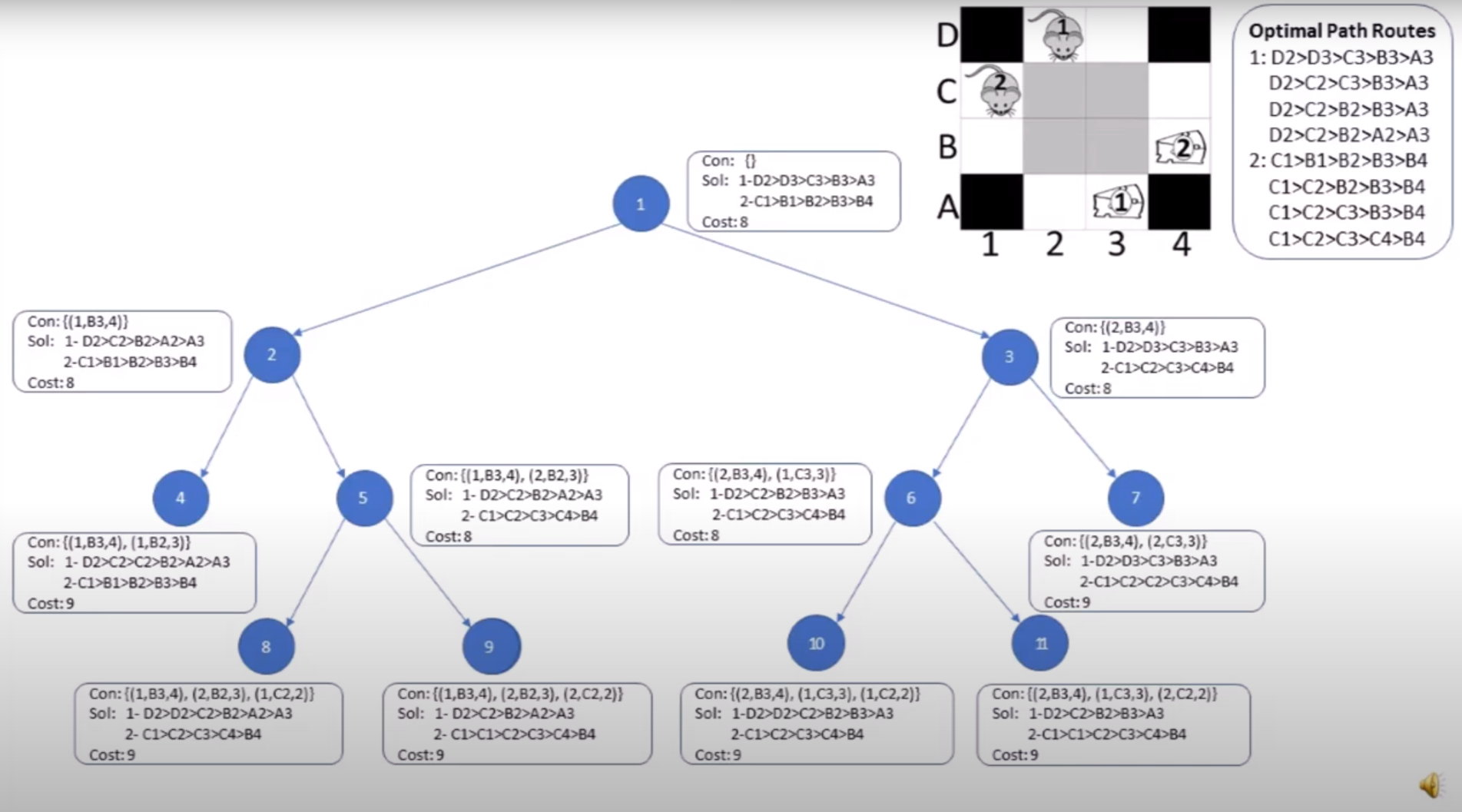
Increasing Cost Tree Search (ICTS)

• Two-level approach
  • Top level: tree search, find the optimal set of path costs; Init (root) : best path for each agent
  • Low level: single-agent path that has the same cost as the top level solution (terminates when non-conflicting solution is found)

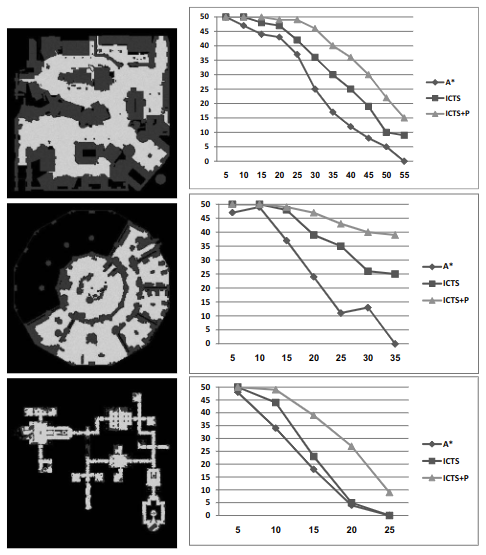
• Advantage

  • performs well when there are many chunks of open area;

• Disadvantage:

  • performs bad when environment is dense;
  • exponential number of paths of cost $C_i$ for low level search

  Computation time

$k$ number of agents; $k^{‘}$ average effective number of agents (number of agents in the largest independent subgroup found by ID)

A* : A* + OD + ID

ICTS + Pairwise pruning:

• avoid low-level search by considering subproblems of paris of agents
• First solve 2-agent search in MDD. If no solution found, this ICTS node has no solution.

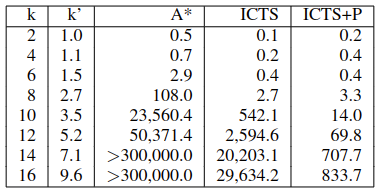
time limit 5 min

[Improvement] Low level results (paths) can be stored in Multi-Valued Decision Diagrams (MDD) , efficient for storing exponentially growing number of paths in linear space

$f: P_1 \times P_2 \times P_3 \times \cdots \times P_k \rightarrow P$

Suboptimal ICTS

• Increase cost of all agents (ICTS only increase a single agent’s cost)
• Makespan: maximum (optimal single-agent path cost) of all agents 用最大完成时间去初始化

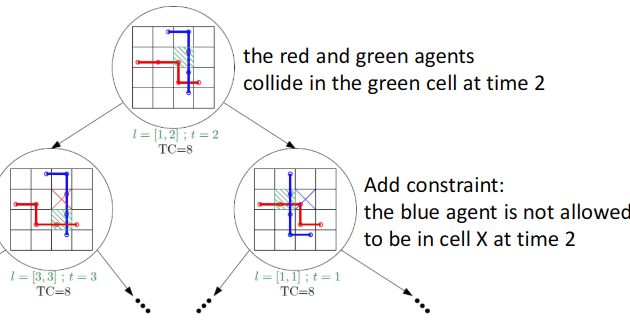
Conflict-based Search (CBS)

• Two level algorithm

  • Low level: optimal A* solution
  • High level: search for a set of constraints to ensure optimal on a tree

  

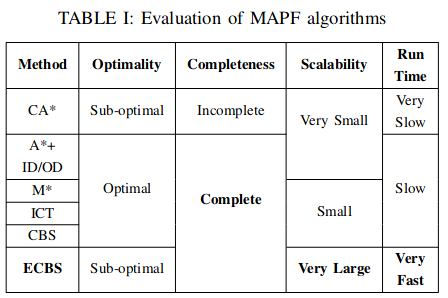
Comparison

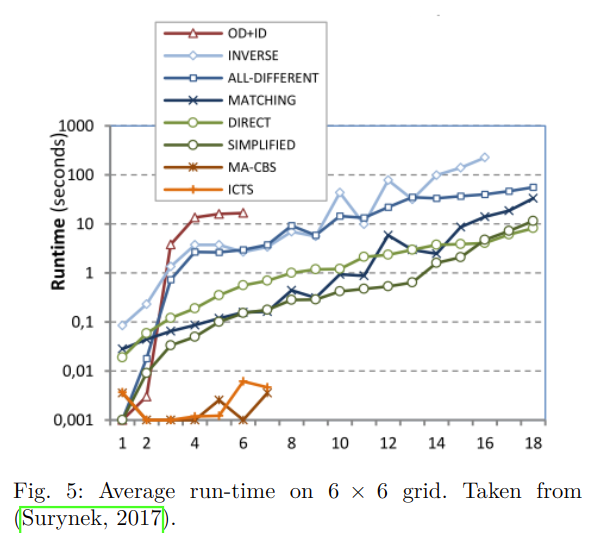
OD+ID; MA-CBS; ICTS; 5-different variant of SAT

Different Multi Agent Path Finding (images/MAPF) algorithms

Algorithm	Optimal	Setting	Completeness	Coupled/Decoupled	Runtime
CA*	No	Centralized	Incomplete	Decoupled	Very Slow
A* + ID/OD	Yes	Centralized	Complete	Sub-dimensional expansion	Slow
CBS	Yes	Centralized	Complete	Coupled	Faster
ICTS	Yes	Centralized	Complete	Coupled	Faster

complete: guarantee to either find a path or to determine no solution.